We will explain this by following the design of a hypothetical vehicle.
The first thing we need to do is deciding the shape of the collision geometry. And here there many options, it could be as simple as box covering the vehicle extends, an aggregate of collision primitives, or a convex hull. For this hypothetical vehicle we will used a convex hull.
The next step is to calculate the weight distribution for the car. This is important because weight distribution is one of the mayor factors in vehicle behavior. In all Newton tutorials the vehicle center is set arbitrarily at the origin or the collision primitive, but like we said before the focus of the tutorials is to demonstrate how to used the API, no how to make a vehicle.
The weight distribution is determined by the mass center, and the moment of inertia of the vehicle, and for correct behavior it is important they are set properly.
Now even thought there are methods for calculating the currect moment of inertial of a homogeneous shape, those methods are of very little practical used for computing the inertia of composite bodies like a vehicle, because these bodies are made of many different components fastened together. It is much simpler and more correct to use the central axis theorem and the approximation of known shapes to calculate the inertia and the center of mass of a vehicle.
First we will layout some familiar shapes on top of the body like this.
notice that these are not collision shapes, just imaginary shapes to help in the calculation.
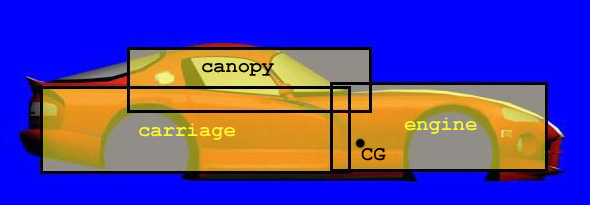
From the sketch the first thing is to calculate the total mass
- Code: Select all
Mt = M1 + M2 + …..
The sume of all the masses of all subparts
M1 can be the engine
M2 can be the canopy, etc
Now we need to calculate the body center of mass, this is a two step process.
- Code: Select all
xc = (x1 * m1 + x2 * m2 + ….) / (m1 + m2 + ….)
yc = (y1 * m1 + y2 * m2 + ….) / (m1 + m2 + ….)
zc = (z1 * m1 + z2 * m2 + ….) / (m1 + m2 + ….)
x1, y1, z1 is the center of part1, and m1 is the mass of part one and so on
With the values we get for xc, yc, zc
We need to preprocess all of the vertices of the geometry shape, before we call the function create convex hull
- Code: Select all
For each vertex in convex Hull point cloud do
x[i] = x[i] – xc;
y[i] = y[i] – yc;
z[i] = z[i] – yc;
this will make the point cloud centered at the calculated origin.
Now wi make translation matrix
- Code: Select all
Matrix = identity matrix
Matrox.posit.x = xc;
Matrox.posit.y = yc;
Matrox.posit.z = zc;
Now we create the collision primitive with this matrix as the offset matrix.
This will have the effect that the origin of the Newton offset will be at the point
xc, yc, zc, and the geometry will be currently aligned to the graphical object.
Finally we need to set the proper moment of inertial, notice that in Newton all rigid bodies are assumed to be aligned to the principal axis of inertia, this is and assumption that is truth for must practical bodies as they have one or two axis of symmetry, for arbitrary shape the application can used the Covariance theorem to calculate the offset matrix of the shape but this is a more advance subject that we may cover in another FAQ.
The Ixx for the new body will be
- Code: Select all
Ixx = Ixx1 + Ixx2 + …. + m1 * x1^2 + m2 * x2 ^ 2 + ……
Iyy = Iyy1 + Iyy2 + …. + m1 * y1^2 + m2 * y2 ^ 2 + ……
Izz = Izz1 + Izz2 + …. + m1 * z1^2 + m2 * z2 ^ 2 + ……
Ixx1, is the inertia of part 1, and so on

